Heron’s Formula TI-84 Program
From here you can either download the program for free onto your computer and then on to your calculator. (don’t worry we’ll walk you through it). Or you can use method 2 and type the code into your calculator by hand. After that, keep scrolling on this page for instructions on what the program does and how to use it.
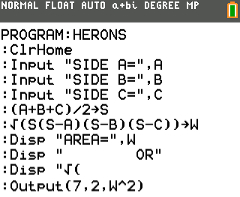
Heron’s Formula Program Code
Method 1 (Download)
1. To download the program click the link below.
2. Click <here> for a tutorial on how to get the program on to your calculator after you have downloaded the file.
3. Keep scrolling to see how the program works and how to use it (optional).
4. The program is currently stored in your calculator’s ram. Click <here> to see a tutorial on how to save the program permanently.
Method 2 (Type)
1. See how to start a program on your calculator click <here> (optional).
2. Begin typing in the code shown in the video or image below.
Do NOT individually type in the colons, or the “PROGRAM:EXAMPLE” name, the colons will show up automatically when you start a new line by pressing [enter]. The “PROGRAM:EXAMPLE” will already be at the top.
Having trouble finding the character or function you see in the code? See how to type any function/character/symbol on your TI-84 Plus>>.
*WARNING*: If you clear the ram on your calculator the program will be lost. To see how to save your work permanently click <here>.
How To Use The Heron’s Formula Solver Program
Heron’s formula allows us to find the area of any triangle by using just the 3 side lengths. For our example, we will find the area of the triangle below.
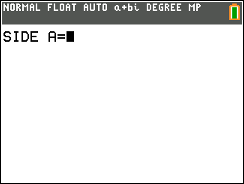
First, start the program by pressing the [prgm] key and scrolling to “HERONS” or whatever you named your version and then press [enter]. After doing that the program should take you to the screen below.
Then from here you can simply enter the tree side lengths of your triangle.
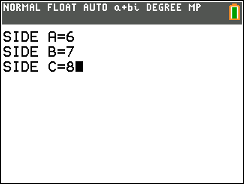
Once you have done that, just press [enter] and you’re done. The calculator will show you the screen below.
As you can see you get the area in two different forms, the decimal answer (20.333) and the exact square root (√413.4375). Both are correct, you will probably more commonly use the first answer form though.
Any questions may be left in the comment section below, they will be answered within 24 hours.
See next…
The top 5 graphing calculators for 2018 with detailed reviews >>
This Calculator Can Factor, Solve, and Give Exact Answers. See Review >>
